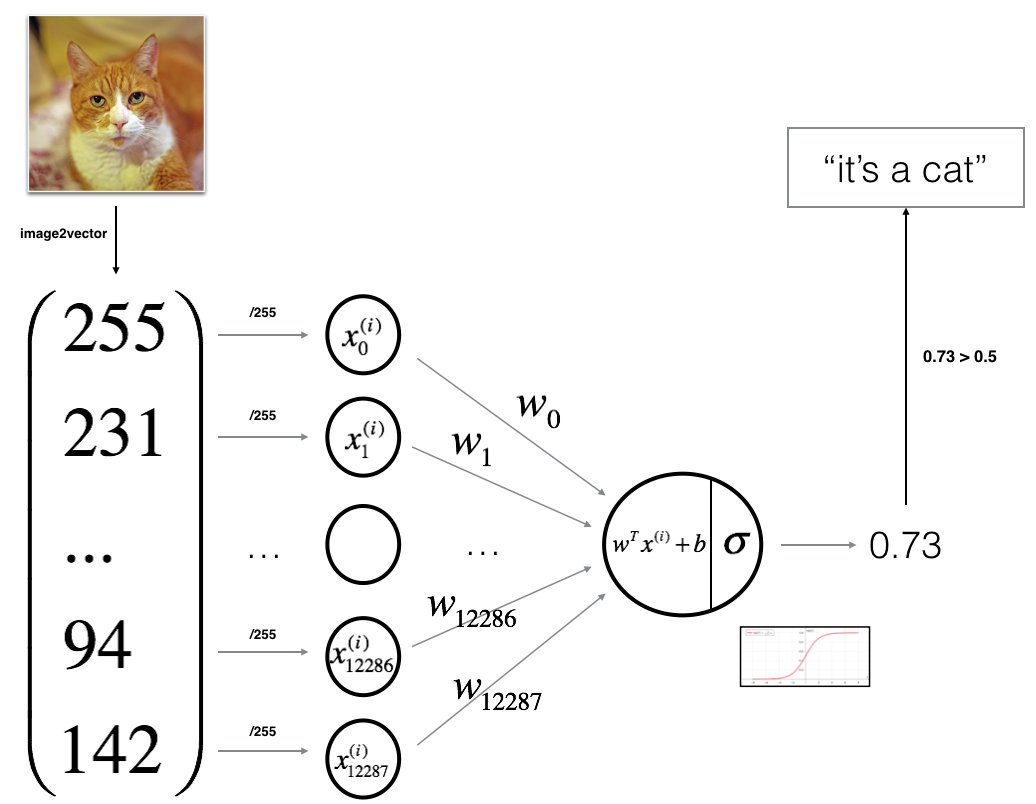
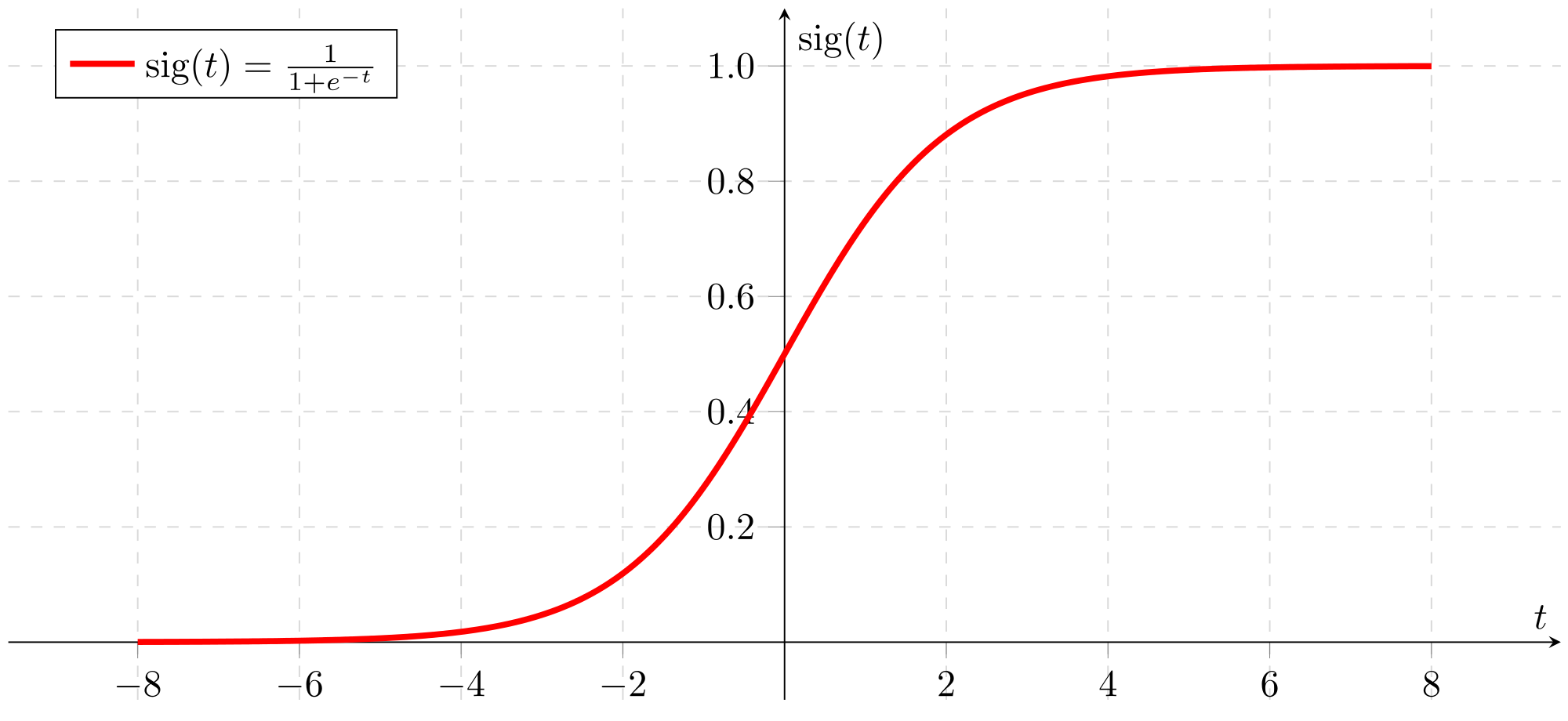
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
|
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def sigmoid(z):
"""
Compute the sigmoid of z
:param z: A scalar or numpy array of any size.
:return: sigmoid(z)
"""
s = 1.0 / (1 + np.exp(-1 * z))
return s
class LogisticRegression(object):
def __init__(self, num_iterations=2000, learning_rate=0.001, print_cost=False):
"""
Builds the logistic regression model
:param num_iterations: hyperparameter representing the number of iterations to optimize the parameters
:param learning_rate: hyperparameter representing the learning rate when update the parameters
:param print_cost: Set to true to print the cost every 100 iterations
"""
self.n_iter = num_iterations
self.learn_rate = learning_rate
self.print_cost = print_cost
self.w = None
self.b = None
def __initialize_with_zeros(self, dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
:param dim: size of the w vector we want
:return: w -- initialized vector of shape (dim, 1); b -- initialized scalar (corresponds to the bias)
"""
w = np.zeros((dim, 1))
b = 0
assert (w.shape == (dim, 1))
assert (isinstance(b, float) or isinstance(b, int))
return w, b
def __propagate(self, X, Y):
"""
Implement the cost function and its gradient for the propagation
:param X: input data
:param Y: label vector
:return: grads --- results of backward propagation; cost --- results of forward propagation
"""
m = X.shape[1]
Z = np.dot(self.w.T, X) + self.b
A = sigmoid(Z)
cost = -1 / m * (np.dot(Y, np.log(A).T) + np.dot(1 - Y, np.log((1 - A)).T))
dw = 1 / m * (np.dot(X, (A - Y).T))
db = np.sum(A - Y) / m
assert (dw.shape == self.w.shape)
assert (db.dtype == float)
cost = np.squeeze(cost)
assert (cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
def fit(self, X_train, Y_train):
"""
This function optimizes w and b by running a gradient descent algorithm
:param X_train: input data
:param Y_train: label vector
:return: costs -- list of all the costs computed during the optimization
"""
self.w, self.b = self.__initialize_with_zeros(X_train.shape[0])
costs = []
for i in range(self.n_iter):
grads, cost = self.__propagate(X_train, Y_train)
dw = grads["dw"]
db = grads["db"]
self.w -= self.learn_rate * dw
self.b -= self.learn_rate * db
if i % 100 == 0:
costs.append(cost)
if self.print_cost and i % 100 == 0:
print("Cost after iteration %i: %f" % (i, cost))
return costs
def predict(self, X_test):
"""
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
:param X_test: input data
:return: Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X_test
"""
m = X_test.shape[1]
Y_prediction = np.zeros((1, m))
w = self.w.reshape(X_test.shape[0], 1)
A = sigmoid(np.dot(w.T, X_test) + self.b)
Y_prediction = np.where(A > 0.5, [1], [0])
assert (Y_prediction.shape == (1, m))
return Y_prediction
if __name__ == "__main__":
train_size = 150
df = pd.read_csv("iris.csv", header=None)
Y_train = df.loc[0:train_size - 1, 4].values
Y_train = np.where(Y_train == "Iris-setosa", [1], [0])
Y_train = Y_train.reshape((1, train_size))
X_train = df.loc[0:train_size - 1, [0, 2]].values
feature1_min, feature1_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
feature2_min, feature2_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
X_train = X_train.T.reshape((2, train_size))
clf = LogisticRegression(num_iterations=2000, learning_rate=0.001, print_cost=True)
clf.fit(X_train, Y_train)
xx1, xx2 = np.meshgrid(np.arange(feature1_min, feature1_max, 0.02), np.arange(feature2_min, feature2_max, 0.02))
X_test = np.array([xx1.ravel(), xx2.ravel()])
Y_prediction = clf.predict(X_test)
Y_prediction = Y_prediction.reshape(xx1.shape)
markers = ('s', 'x')
colors = ("red", "blue")
plt.contourf(xx1, xx2, Y_prediction, c="gray")
plt.xlim(feature1_min, feature1_max)
plt.ylim(feature2_min, feature2_max)
for idx, y_train in enumerate(np.unique(Y_train)):
plt.scatter(x=X_train[0, np.squeeze(Y_train == y_train)], y=X_train[1, np.squeeze(Y_train == y_train)],
alpha=0.8, c=colors[idx],
marker=markers[idx], label=y_train)
plt.xlabel(u"花瓣长度", fontproperties='SimHei')
plt.ylabel(u"花茎长度", fontproperties='SimHei')
plt.legend(loc="upper left")
plt.show()
|